有关各种RAID技术的讨论一直在各个厂商以及用户之间争执不休,好象做存储的,张口闭口都会说自家的RAID技术实现起来多么多么好,别家的技术有多大多大的缺陷,但有多少人真正了解RAID技术的实质呢?好在有DoSTOR这个大平台,可以帮助大家解惑,本次我们就请来DoSTOR特约技术专家董唯元先生,深入浅出的告诉各位,RAID-6是什么。
既然是讲原理,那些“为什么需要RAID6”、“RAID6的优势”等内容就都省去了。直接进入枯燥无趣的理论。
一、RAID5和XOR运算
为了照顾初学者,还是先把相关基本概念介绍一下,老手可以跳过这部分直接看下面。(别低头!是看本帖下面,想些什么呐~)
XOR运算是数理逻辑的基本运算之一,在课本上的符号是一个圆圈里面一个加号。实在懒得用插入符号功能,大家就凑合着看吧。
两个数字之间的XOR运算定义是:
- 1 XOR 1 = 0
- 1 XOR 0 = 1
- 0 XOR 1 = 1
- 0 XOR 0 = 0
(忽然想起试行新车牌的时候,有些深圳人用三位二进制数标记性别。010是男的,101是女的。Sorry,扯远了。)
多个数字XOR的时候,有两个特点:
- A)结果与运算顺序无关。也就是 (a XOR b) XOR c = a XOR (b XOR c)。
- B)各个参与运算的数字与结果循环对称。如果 a XOR b XOR c = d,那么a = b XOR c XOR d;b = a XOR c XOR d;c = a XOR b XOR d。
磁盘阵列中的RAID5之所以能够容错,就是利用了XOR运算的这些特点。上面例子中的a、b、c、d就可以看作是四颗磁盘上的数据,其中三个是应用数据,剩下一个是校验。碰到故障的时候,甭管哪个找不到了,都可以用剩下的三个数字XOR一下算出来。
在实际应用中,阵列控制器一般要先把磁盘分成很多条带(英文叫Stripe,注意不是Stripper),然后再对每组条带做XOR。
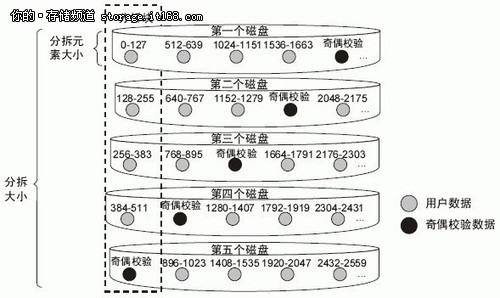
见下面第一个图:

- P1 = 数据a XOR 数据b XOR 数据c
- P2 = 数据d XOR 数据e XOR 数据f
- P3 = 数据g XOR 数据h XOR 数据i
- P4 = 数据j XOR 数据k XOR 数据l
扫盲部分就讲这么多,再不懂就google吧,满山遍野都是RAID5算法的介绍。
二、RAID6和Reed-Solomon编码
本来想写成“李德-所罗门编码”,但那样就不方便大家一边看帖子一边google了。Reed-Solomon编码是通讯领域中经常碰到的一个算法,已经有15年以上的历史了。(靠!讲存储嘛,跟通讯有个鸟关系?)
其实很多校验算法都是通讯领域最先研究出来,然后才应用到其他领域的。前面说到的XOR算法对一组数据只能产生一个校验,搞通讯的工程师们觉得不够可靠,于是就研究出很多能对一组数据产生多个校验的算法。Reed-Solomon编码是其中应用最广泛的一个,咱们以前经常用的ADSL、xDSL、高速Modem都有采用。后来手机、卫星电视、数字电视、CD唱片、DVD、条码系统、还有……(有完没完!说存储呢!)连高级点儿的服务器内存也用这个算法做校验和纠错。(总算跟存储沾上点儿边~)
现在存储的工程师也觉得RAID5中只能容忍一颗磁盘离线不够理想,需要一种容忍多颗磁盘离线的技术,自然就会想到Reed-Solomon编码啦。把这种算法应用到存储中,就可以让N颗磁盘的空间装应用数据,M颗磁盘的空间装校验码(对一组N个数据生成M个校验,但实际上校验码是分散在所有磁盘上的),这样只要离线的磁盘不大于M颗,数据就不会丢失。
Reed-Solomon编码理论中有一个公式:
N + M + 1 = 2的b次方(在电脑里写公式真是麻烦!)
其中b是校验字的位数。(校验字是生成校验过程需要用的一个东东,不是最后的校验码。)举例来说,如果用8位的字节做校验字,那么M + N = 255,而RAID6是特指M = 2,这样N = 253。
就是说,用8位字节做校验字的话,理论上一个RAID6的磁盘组可以容下253颗磁盘。
当然啦,实际应用中,太多的磁盘一起做运算会严重影响性能,所以阵列控制器和芯片的设计者都会把磁盘组的容量限制在16颗左右。(做了这么多无聊算术题,还是没提RAID6到底是啥!)喂!喂!别走啊,很快就讲到RAID6的实现啦。
卖了这么多关子,实在是因为RAID6这个概念所指的意义太混乱。从功能上讲,能实现两颗磁盘掉线容错的,都叫RAID6。(至少我认识的销售们都这么认为。)但是实行这一功能的方式却有很多很多。(沉默3分钟)
真的很多!哎哟!别打啊~
Intel的P+Q RAID6,NetApp的RAID-DP,HP的RAID5-DP,还要很多实验室中的原型机都能实行这个功能。但是由于机制不同,各种所谓的RAID6,其性能表现、磁盘负载分布、错误恢复方式都完全不同。
你让我从哪说起好哩?
三、基于P+Q的RAID6
在Intel的80333IOP芯片中,有一个新的引擎叫P+Q单元,是专门用来处理RAID6加速的。详情请查阅Intel官方网站……(鸡蛋、西红柿、拖鞋。咦!这是谁的臭袜子?)
对比RAID5的机制,Intel的P+Q RAID6是这样写磁盘的:
见下面第二个图:

这里每个条带中的P,跟RAID5里面的P意义完全一样,就是同一条带中除Q以外其它数据的XOR运算结果。而Q呢,就是理解这个技术的关键所在了。
咳~咳~听好了。
Q是同一条带中各数据的女朋友们进行XOR运算的结果。别翻白眼啊,书上就是这么写的啊!哦,还是英文的,我翻译给你听。
“把条带中每个数据分别GF一下,然后这些结果再XOR,就得到Q。”(大哥,你到底懂不懂啊!GF是Galois Field的缩写,是法国著名数学奇才伽罗瓦发明的一种数学变换。)
哦,想起来了。伽罗瓦嘛,发明群论的那个。生于法国大革命前,二十出头就英年早逝,还是为了个姑娘跟人决斗被打死的。最著名的成果就是给3次以上方程判了死刑。是我人生第二偶像啊……(唐僧!)
这个GF变换呢,就是这个淘气的伽同学当年为了逃避老师点名,而发明的一种教室换座位方法。按照这种方法,每个人都不会坐在自己的座位上,而且每个人都肯定会有座位。而且任意个同学的座位号进行XOR运算之后,仍然跑不出这个教室里的座位号。(这个伽同学好像很无聊噢!没办法,人家聪明嘛!)
扯太远啦!回到正题。
在Intel 80333IOP中存着两个表格,分别对应GF正向变换和反向变换。任何一个8位二进制数,都可以直接在表格中查到对应的GF变换结果。(我还是想把这个结果说成是源数据的女朋友~)
这两个表格分别在Intel 80333IOP研发手册的第445页和446页,不过我估计大部分人会懒得去看。也是,看了又能怎么样呢?反正Intel已经把那玩意固化到芯片里了。(哇!都半夜2点了,说完P+Q RAID6的恢复,我要先zZZ……了。)
如果一颗磁盘掉线,根本不需要Q用P直接就搞定了,跟RAID5一样。
如果两颗磁盘掉线,又分做两种情况:
- A)坏的地方有Q。这种情况跟RAID5坏一颗磁盘一样,用XOR就恢复了。
- B)坏的地方没有Q。用GF变换加XOR一起搞定。
结合上面表格的例子,如果磁盘5和磁盘6掉线。那条带1和条带2就属于情况A;而条带3、4、5和6属于情况B。
待续
本文版权归作者及DoSTOR所有,如需转载请与本站联系!